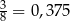/Szkoła średnia

Zadanie nr 9503932

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru liczb 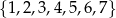{1,2,3,4 ,5 ,6,7} losujemy kolejno bez zwracania dwie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3, jeżeli pierwsza z wylosowanych liczb jest liczbą pierwszą.

Rozwiązanie

W danym zbiorze są cztery liczby pierwsze: 2, 3, 5, 7.

Sposób I

Za zdarzenia elementarne przyjmijmy pary 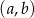(a,b ) wylosowanych liczb. Są więc

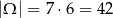
|Ω | = 7⋅6 = 42

zdarzenia elementarne.

Niech 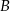B oznacza zdarzenie polegające na otrzymaniu liczby pierwszej przy wyborze pierwszej liczby. Zatem

P(B ) = 4-. 7

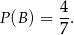
Niech 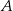A oznacza zdarzenie polegające na otrzymaniu pary liczb 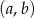(a,b) , w której 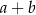a+ b jest liczbą podzielną przez 3. Jest 9 zdarzeń

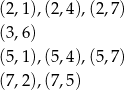
(2,1),(2,4 ),(2 ,7) (3,6) (5,1),(5,4 ),(5 ,7) (7,2),(7,5 )

sprzyjających zdarzeniu 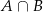A ∩ B , więc

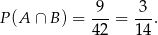
P (A ∩ B) = 9--= 3-. 42 14

Interesujące nas prawdopodobieństwo jest więc równe

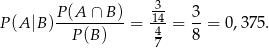
-3 P (A |B )P-(A-∩-B)-= 14-= 3-= 0 ,375. P (B) 4 8 7

Sposób II

Tym razem za zdarzenia elementarne przyjmijmy pary 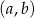(a,b) , w których a jest liczbą pierwszą. Mamy więc

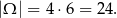
|Ω | = 4 ⋅6 = 24 .

Tak samo jak pierwszym sposobie ustalamy, że jest 9 zdarzeń, w których suma liczb dzieli się przez 3, więc interesujące nas prawdopodobieństwo jest równe

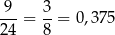
-9-= 3-= 0,375 24 8

 
Odpowiedź: 3 = 0,375 8

Wersja PDF