Zadanie nr 9507173
Funkcja 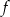 określona jest wzorem
określona jest wzorem 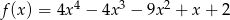 .
.
- Znajdź punkt przecięcia wykresu funkcji
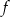 z osia
z osia 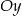 .
. - Znajdź, o ile istnieją, punkty przecięcia funkcji
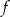 z osia
z osia 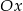 .
. - Wyznacz te argumenty, dla których funkcje
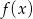 i funkcja
i funkcja 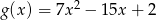 przyjmują tę samą wartość.
przyjmują tę samą wartość.
Rozwiązanie
- Wykres funkcji przecina oś
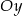 dla
dla 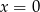 , czyli w punkcie
, czyli w punkcie 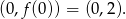
Odpowiedź: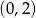
- Musimy rozwiązać równanie
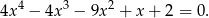
Szukamy najpierw pierwiatków całkowitych, czyli sprawdzamy dzielniki wyrazu wolnego. Łatwo znaleźć pierwiastek
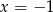 . Dzielimy więc wielomian przez
. Dzielimy więc wielomian przez 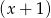 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy. 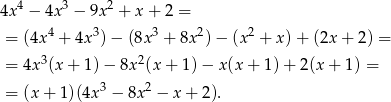
Podobnie jak poprzednio, sprawdzamy dzielniki wyrazu wolnego i znajdujemy pierwiastek
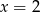 . Dzielimy więc wielomian stopnia 3 przez
. Dzielimy więc wielomian stopnia 3 przez 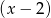 .
. 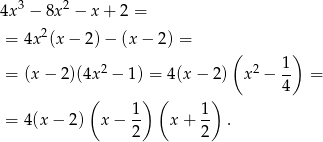
Odpowiedź: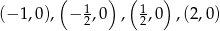
- Musimy rozwiązać równanie
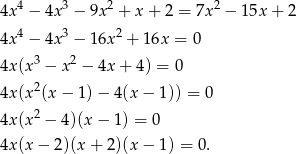
Odpowiedź: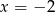 ,
, 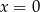 ,
, 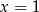 ,
, 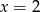
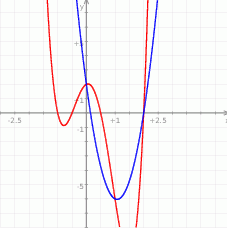
Na koniec, dla ciekawskich, wykresy funkcji 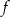 i
i 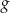 .
.