/Szkoła średnia

Zadanie nr 9515230

Dodaj do ulubionych
Dodaj do rozwiązanych

Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 8 cm, a jego wysokość 12 cm. Połączono środki dwóch sąsiednich krawędzi dolnej podstawy oraz najbardziej odległy od tego odcinka wierzchołek górnej podstawy. Oblicz pole otrzymanego trójkąta.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

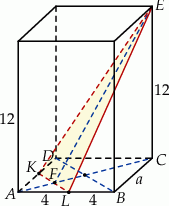
Podstawa 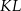KL otrzymanego trójkąta 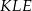KLE jest odcinkiem łączącym środki boków w trójkącie 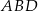ABD , więc

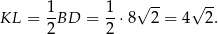
-- -- KL = 1-BD = 1⋅ 8√ 2 = 4√ 2. 2 2

Ponadto

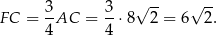
√ -- √ -- FC = 3-AC = 3⋅ 8 2 = 6 2. 4 4

Wysokość 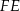FE trójkąta 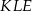KLE obliczamy z trójkąta prostokątnego FCE .

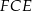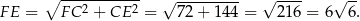
∘ ---2-----2- √ --------- √ ---- √ -- F E = FC + CE = 72+ 144 = 21 6 = 6 6.

Pole przekroju jest więc równe

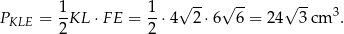
1 1 √ -- √ -- √ -- PKLE = --KL ⋅F E = -⋅ 4 2⋅ 6 6 = 24 3 cm 3. 2 2

 
Odpowiedź: √ -- 3 24 3 cm

Wersja PDF