/Szkoła średnia

Zadanie nr 9521105

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkąt równoramienny 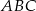ABC , w którym 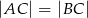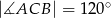|AC | = |BC | , ∘ |∡ACB | = 12 0 , wpisano okrąg, którego promień ma długość r . Oblicz długości boków trójkąta.

Rozwiązanie

Zacznijmy od rysunku i oznaczmy długość podstawy trójkąta przez a .

PIC

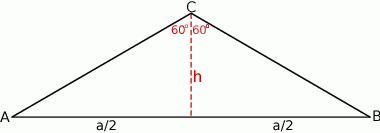
Sposób I

Aby wykorzystać podaną informację o promieniu okręgu wpisanego w trójkąt 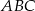ABC , będziemy chcieli skorzystać ze wzoru na pole 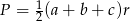P = 1(a + b + c)r 2 . Aby to zrobić musimy obliczyć długość boku 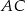AC i pole trójkąta w zależności od a .

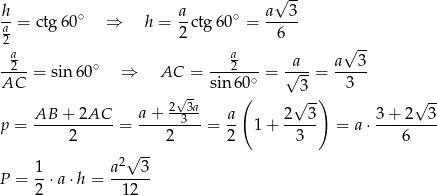
√ -- h-= ctg60 ∘ ⇒ h = a-ctg 60∘ = a--3- a2 2 6 a a √ -- --2- = sin6 0∘ ⇒ AC = ---2---= √a--= a--3- AC sin 60∘ 3 3 2√-3a- ( √ -) √ -- p = AB-+--2AC--= a-+---3--= a- 1+ 2--3- = a ⋅ 3-+-2--3 2 2 2 3 6 √ -- 1- a2--3- P = 2 ⋅a⋅ h = 12

Zatem ze wspomnianego wzoru na pole trójkąta, mamy

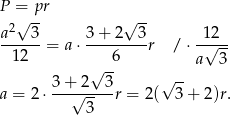
P = pr √ -- √ -- a2--3- 3-+-2--3- -12-- 12 = a ⋅ 6 r / ⋅ √ -- √ -- a 3 3-+-2---3 √ -- a = 2 ⋅ √ 3- r = 2( 3 + 2)r.

Stąd

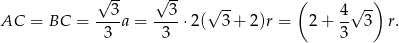
√ -- √ -- 3 3 √ -- ( 4√ --) AC = BC = ---a = ----⋅2( 3 + 2)r = 2+ -- 3 r. 3 3 3

Sposób II

Połączmy środek 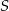S okręgu wpisanego w trójkąt 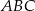ABC z punktami styczności tego okręgu z bokami i przyjmijmy oznaczenia z rysunku.

PIC

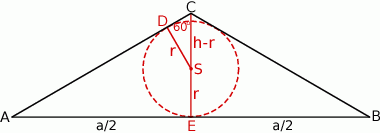
W trójkącie prostokątnym 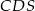CDS mamy

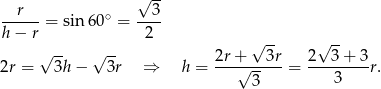
√ -- --r-- = sin 60∘ = --3- h − r 2 -- -- √ -- √ -- 2r + √ 3r 2√ 3 + 3 2r = 3h − 3r ⇒ h = ---√------= --------r. 3 3

Patrzymy teraz na trójkąt prostokątny 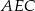AEC .

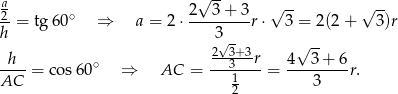
√ -- a 2 3+ 3 √ -- √ -- 2-= tg 60∘ ⇒ a = 2⋅ --------r ⋅ 3 = 2(2 + 3)r h 3√- √ -- h 2-3+3-r 4 3 + 6 ----= cos60 ∘ ⇒ AC = --31---= ---------r. AC 2 3

 
Odpowiedź: 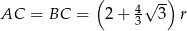( √ -) AC = BC = 2 + 43 3 r , √ -- AB = 2( 3 + 2)r

Wersja PDF