/Szkoła średnia
Lubelska próba przed maturą
z matematyki poziom rozszerzony 10 marca 2020 Czas pracy: 180 minut
Zadania zamknięte
Wskaż 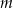 , dla którego rozwiązaniem równania
, dla którego rozwiązaniem równania 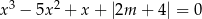 jest liczba 2.
jest liczba 2.
A) 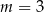 lub
lub 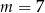 B)
B)  lub
lub 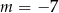
C) 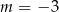 lub
lub 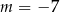 D)
D) 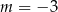 lub
lub 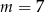
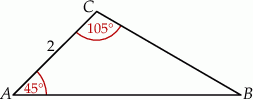
Pole trójkąta  przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
A) 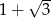 B)
B) 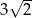 C)
C) 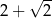 D)
D) 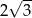
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie 8 i ramieniu 10. Powierzchnia boczna stożka jest wycinkiem koła o kącie środkowym
A) 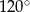 B)
B) 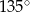 C)
C) 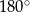 D)
D) 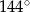
Najmniejszym rozwiązaniem równania 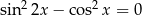 w przedziale
w przedziale 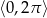 jest liczba A)
jest liczba A) 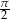 B)
B) 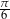 C)
C) 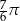 D)
D) 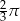
Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Poprowadzono wysokość na przeciwprostokątną. Wysokość ta podzieliła przeciwprostokątną na odcinki w stosunku
A) 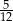 B)
B) 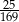 C)
C) 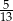 D)
D) 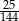
Zadania otwarte
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 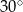 . Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Liczba  z dzielenia przez 4 daje resztę 1. Liczba
z dzielenia przez 4 daje resztę 1. Liczba 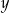 z dzielenia przez 4 daje resztę 3. Wyznacz resztę z dzielenia liczby
z dzielenia przez 4 daje resztę 3. Wyznacz resztę z dzielenia liczby 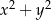 przez 8.
przez 8.
Wykaż, że jeżeli 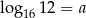 , to
, to 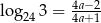 .
.
Oblicz, ile jest czterocyfrowych liczb naturalnych parzystych, w których występuje dokładnie jedno zero.
Wyznacz dziedzinę funkcji 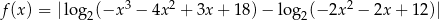 .
.
Wyznacz iloraz nieskończonego, zbieżnego ciągu geometrycznego, w którym pierwszy wyraz jest równy 6, a suma wszystkich wyrazów tego ciągu stanowi 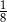 sumy ich kwadratów.
sumy ich kwadratów.
W dany trapez można wpisać okrąg i jednocześnie można na tym trapezie opisać okrąg. Wysokość tego trapezu jest równa 8, a jego kąt ostry ma miarę 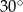 . Oblicz długość promienia okręgu opisanego na tym trapezie.
. Oblicz długość promienia okręgu opisanego na tym trapezie.
Dany jest trójkąt 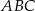 o wierzchołkach:
o wierzchołkach: 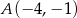 ,
, 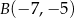 ,
, 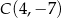 . Oblicz długość odcinka
. Oblicz długość odcinka 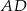 dwusiecznej kąta przy wierzchołku
dwusiecznej kąta przy wierzchołku 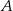 .
.
Wykresy funkcji kwadratowych 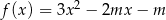 oraz
oraz 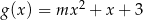 , dla
, dla 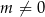 , przecinają się w dwóch punktach. Wyznacz wszystkie wartości
, przecinają się w dwóch punktach. Wyznacz wszystkie wartości 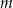 , dla których iloraz sumy odciętych tych punktów przez ich iloczyn jest o
, dla których iloraz sumy odciętych tych punktów przez ich iloczyn jest o  mniejszy od największej wartości funkcji
mniejszy od największej wartości funkcji 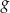 .
.
W ostrosłupie prawidłowym czworokątnym pole podstawy jest dwa razy większe od pola ściany bocznej. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa.
Dana jest parabola o równaniu 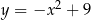 . Na tej paraboli leży punkt
. Na tej paraboli leży punkt 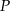 o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie
o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie 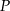 ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu.
ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu.

