/Szkoła średnia

Zadanie nr 9540808

Dodaj do ulubionych
Dodaj do rozwiązanych

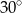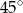Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 30∘ i 45 ∘ . Oblicz wysokość tego trapezu.

Rozwiązanie

Zacznijmy od rysunku.

PIC

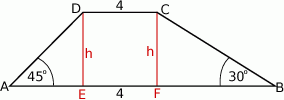
Sposób I

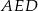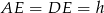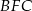Trójkąt AED to połówka kwadratu, więc AE = DE = h , a trójkąt BF C to połówka trójkąta równobocznego o boku 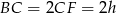BC = 2CF = 2h , więc

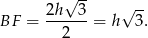
√ -- 2h---3 √ -- BF = 2 = h 3 .

Mamy zatem

√ -- 10 = AB = AE + EF + FB = h+ 4+ h 3 √ -- h + h 3 = 6 h(1 + √ 3) = 6 √ -- 6 6( 3 − 1) √ -- h = √-------= ---3−--1---= 3 3 − 3. 3+ 1

Sposób II

Jeżeli oznaczymy szukaną długość wysokości przez 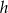h , to mamy

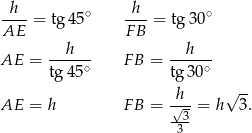
-h--= tg 45∘ -h- = tg 30∘ AE FB h h AE = -----∘ FB = -----∘ tg 45 tg30 √h- √ -- AE = h FB = --3 = h 3 . 3

Stąd

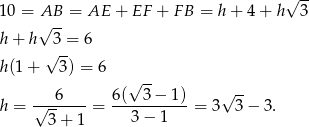
√ -- 10 = A√B--= AE + EF + FB = h+ 4+ h 3 h + h 3 = 6 √ -- h(1 + 3) = 6 √ -- √ -- h = √--6----= 6(--3-−-1)-= 3 3 − 3. 3+ 1 3− 1

 
Odpowiedź: 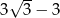√ -- 3 3 − 3 cm

Wersja PDF