/Szkoła średnia

Zadanie nr 9550934

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole rombu o kącie ostrym 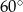∘ 60 jest równe 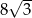√ -- 8 3 . Bok tego rombu ma długość
A) 6 B) 2 C) 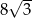√ -- 8 3 D) 4

Rozwiązanie

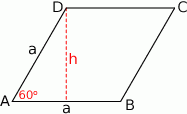
Oznaczmy długość boku rombu przez a .

PIC

Sposób I

Wyliczamy wysokość rombu

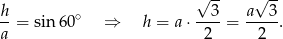
√ -- √ -- h-= sin 60∘ ⇒ h = a⋅ --3-= a--3-. a 2 2

Zatem pole rombu jest równe

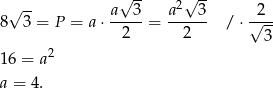
√ -- 2√ -- √ -- a--3- a---3- √2-- 8 3 = P = a ⋅ 2 = 2 / ⋅ 3 2 16 = a a = 4.

Sposób II

Korzystamy ze wzoru na pole równoległoboku z sinusem

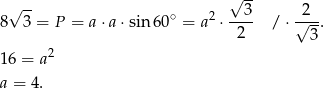
√ -- √ -- 8 3 = P = a ⋅a⋅sin 60∘ = a2 ⋅--3- / ⋅√2--. 2 3 16 = a2 a = 4.

 
Odpowiedź: D

Wersja PDF