Zadanie nr 9563344
Rozwiąż nierówność 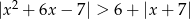 .
.
Rozwiązanie
Sprawdźmy najpierw jakie są pierwiastki trójmianu w pierwszej wartości bezwzględnej.
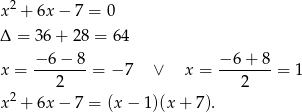
W takim razie musimy rozważyć 3 przypadki.
Jeżeli 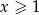 to mamy nierówność
to mamy nierówność
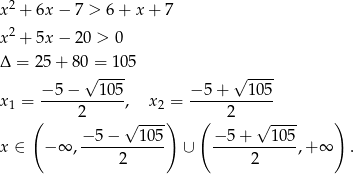
Ponieważ 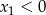 i
i 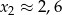 , w połączeniu z warunkiem
, w połączeniu z warunkiem 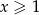 otrzymujemy w tym przypadku
otrzymujemy w tym przypadku 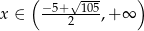 .
.
Jeżeli 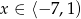 to mamy nierówność
to mamy nierówność
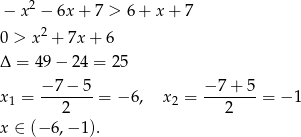
Przedział ten w całości zawiera się w przedziale 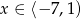 .
.
Jeżeli wreszcie 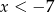 to mamy nierówność
to mamy nierówność
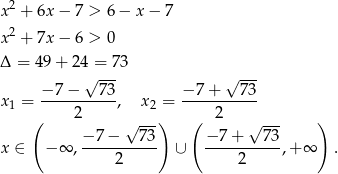
Ponieważ 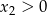 i
i 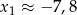 w połączeniu z warunkiem
w połączeniu z warunkiem 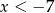 otrzymujemy w tym przypadku
otrzymujemy w tym przypadku 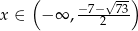 .
.
Odpowiedź: