/Szkoła średnia

Zadanie nr 9581075

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków trójkąta prostokątnego, którego obwód jest równy 24cm tworzą ciąg arytmetyczny. Oblicz

  • długość wysokości poprowadzonej z wierzchołka kąta prostego;
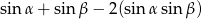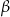  • wartość wyrażenia sinα + sin β − 2(sinα sinβ ) , gdzie α i β – miary kątów ostrych trójkąta.

Rozwiązanie

  • Jeżeli oznaczymy boki trójkąta przez 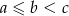a ≤ b < c , to z podanych informacji mamy układ równań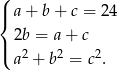
    ( | a + b + c = 2 4 { | 2b = a+ c ( a 2 + b2 = c2.
    PIC

    Podstawiając za 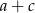a+ c z drugiego równania do pierwszego, mamy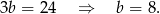

    3b = 24 ⇒ b = 8.

    Pozostają nam więc dwa równania

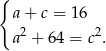
    { a + c = 16 a2 + 64 = c2.

    Podstawiamy 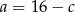a = 16 − c do drugiego równania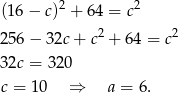

    (16 − c)2 + 64 = c2 2 2 25 6− 32c+ c + 6 4 = c 32c = 320 c = 10 ⇒ a = 6.

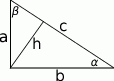
    Aby obliczyć szukaną długość wysokości 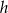h opuszczonej na przeciwprostokątną, skorzystamy z dwóch wzorów na pole trójkąta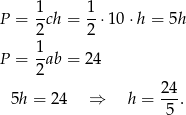

    1 1 P = -ch = --⋅10⋅ h = 5h 2 2 P = 1ab = 2 4 2 24 5h = 24 ⇒ h = 5-.

     
    Odpowiedź: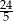 254

  • Z poprzedniego podpunktu wiemy, że
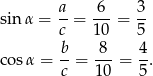
    a- -6- 3- sin α = c = 10 = 5 b 8 4 co sα = --= ---= --. c 10 5

    Liczymy

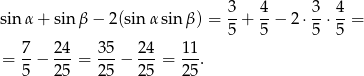
    3 4 3 4 sinα + sin β− 2(sinα sinβ ) = --+ --− 2⋅ -⋅ --= 5 5 5 5 7- 24- 35- 24- 11- = 5 − 25 = 25 − 25 = 25.

     
    Odpowiedź: 11 25

Wersja PDF