Zadanie nr 9582491
Rozwiąż równanie 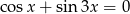 .
.
Rozwiązanie
Korzystamy ze wzoru
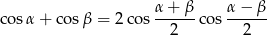
na sumę cosinusów.
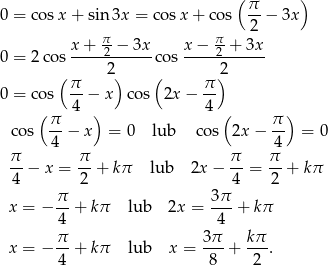
Odpowiedź: 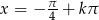 lub
lub 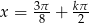 ,
, 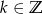
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 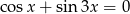 .
.
Korzystamy ze wzoru
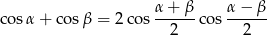
na sumę cosinusów.
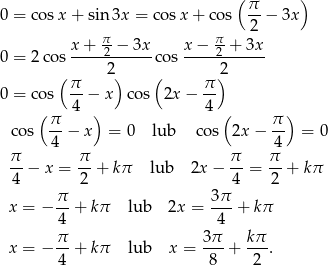
Odpowiedź: 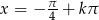 lub
lub 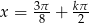 ,
,