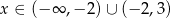/Szkoła średnia

Zadanie nr 9598692

Dodaj do ulubionych
Dodaj do rozwiązanych

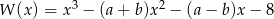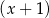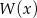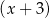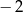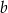Wielomian 3 2 W (x) = x − (a+ b )x − (a − b )x − 8 jest podzielny przez dwumian (x+ 1) , a reszta z dzielenia wielomianu W (x) przez dwumian (x + 3) wynosi − 2 . Oblicz a i b , a następnie rozwiąż nierówność W (x) < 4 .

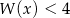Rozwiązanie

Podane informacje o podzielnościach prowadzą układu równań

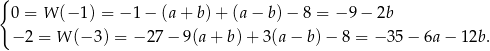
{ 0 = W (− 1) = −1 − (a + b) + (a − b) − 8 = − 9 − 2b − 2 = W (− 3) = − 27 − 9 (a+ b )+ 3(a − b) − 8 = −3 5− 6a− 12b.

Z pierwszego równania mamy 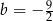b = − 92 , a z drugiego

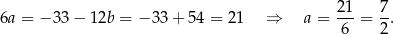
6a = − 33 − 12b = − 33+ 54 = 21 ⇒ a = 21-= 7-. 6 2

Zatem

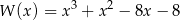
3 2 W (x) = x + x − 8x − 8

i pozostało rozwiązać nierówność

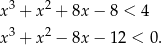
3 2 x + x + 8x − 8 < 4 x3 + x2 − 8x − 12 < 0 .

Szukamy teraz pierwiastków wymiernych lewej strony – łatwo zauważyć, że jednym z nich jest 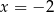x = − 2 . Dzielimy więc wielomian z lewej strony nierówności przez 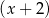(x+ 2) . My jak zwykle zrobimy to grupując wyrazy.

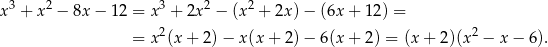
x3 + x2 − 8x − 12 = x3 + 2x2 − (x2 + 2x)− (6x + 12) = 2 2 = x (x+ 2)− x(x + 2) − 6(x + 2) = (x + 2 )(x − x− 6).

Rozkładamy jeszcze trójmian w nawiasie.

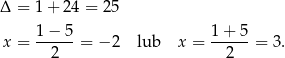
Δ = 1 + 24 = 2 5 1 − 5 1 + 5 x = ------= − 2 lub x = ------= 3. 2 2

Interesująca nas nierówność przyjmuje więc postać

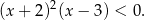
2 (x + 2) (x − 3) < 0.

Jej rozwiązaniem jest zbiór

x ∈ (− ∞ ,− 2)∪ (− 2,3 ).

 
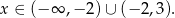
Odpowiedź: 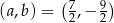( ) (a,b) = 72,− 92 , x ∈ (− ∞ ,− 2) ∪ (− 2,3)

Wersja PDF