Zadanie nr 9602139
W urnie jest 7 kul czarnych i 5 białych. Sześć z nich przekładamy do drugiej urny, początkowo pustej, i z niej losujemy 2 kule bez zwracania. Jakie jest prawdopodobieństwo, że druga z nich będzie biała.
Rozwiązanie
Zadanie można oczywiście rozwiązać ze wzorów na prawdopodobieństwo całkowite/warunkowe (zastanawiając się ile w pierwszym kroku wybierzemy kul białych), ale ta droga jest dość uciążliwa rachunkowo.
Zamiast tego, zastanówmy się o co tak naprawdę chodzi.
Sposób I
Wybieramy sześć kul, z nich dwie, a potem jedną. Efekt jest taki, że spośród 12 kul wybraliśmy jedną kulę. Twierdzimy, że jest to dokładnie to co się stało, tzn., że prawdopodobieństwo wynosi
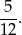
Aby się o tym przekonać, wygodnie jest myśleć od końca. Jak policzyć prawdopodobieństwo wylosowania białej kuli spośród wszystkich 12? Można jak przed chwilą, ale można rzecz skomplikować i powiedzieć, że najpierw losujemy 6, a potem z nich jedną. To, że prawdopodobieństwa w obu sytuacjach są takie same, to dokładnie wzór na prawdopodobieństwo całkowite (lub zdrowy rozsądek). Dalej tak samo, prawdopodobieństwo wybrania białej kuli z 6, to to samo, co wybrać dwie i z nich jedną – znowu wzór na prawdopodobieństwo całkowite.
Osoby, które nie czują się przekonane powyższym komentarzem mogą spróbować sobie to policzyć następująco. Niech 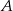 będzie zdarzeniem polegającym na wylosowaniu białej kuli spośród wszystkich 12. Oczywiście
będzie zdarzeniem polegającym na wylosowaniu białej kuli spośród wszystkich 12. Oczywiście 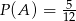 . Niech teraz
. Niech teraz 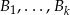 będą wszystkimi możliwymi zdarzeniami polegającymi na usunięciu z urny
będą wszystkimi możliwymi zdarzeniami polegającymi na usunięciu z urny 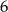 kul. Na mocy wzoru na prawdopodobieństwo całkowite mamy
kul. Na mocy wzoru na prawdopodobieństwo całkowite mamy
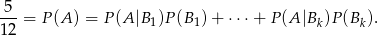
Teraz jest ważny moment: jakie zdarzenie opisuje prawa strona? Każde 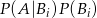 jest prawdopodobieństwem wylosowania (ustalonej) szóstki liczb (tej, która zostaje w urnie) i losowaniem z tej szóstki białej kuli. Mamy więc dokładnie sytuację: losujemy 6 kul i z nich wybieramy białą (można myśleć o gałęziach drzewka).
jest prawdopodobieństwem wylosowania (ustalonej) szóstki liczb (tej, która zostaje w urnie) i losowaniem z tej szóstki białej kuli. Mamy więc dokładnie sytuację: losujemy 6 kul i z nich wybieramy białą (można myśleć o gałęziach drzewka).
Pozostało teraz stwierdzić, że losowanie białej kuli z 6, to to samo, co wylosować 2 i patrzeć czy druga jest biała. Myślimy podobnie jak poprzednio: niech 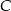 będzie zdarzeniem polegającym na wybraniu białej kuli z 6, a
będzie zdarzeniem polegającym na wybraniu białej kuli z 6, a 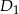 i
i 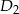 zdarzeniami polegającymi na usunięciu odpowiednio białej i czarnej kuli z urny. Mamy wtedy
zdarzeniami polegającymi na usunięciu odpowiednio białej i czarnej kuli z urny. Mamy wtedy
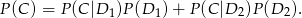
Co opisują prawdopodobieństwa z prawej strony? – są to dokładnie prawdopodobieństwa otrzymania drugiej kuli białej w parze, jeżeli na pierwszym miejscu wybraliśmy odpowiednio białą i czarną kulę (to jest ta usunięta z urny).
Trudność tego zadania polega na tym, że stosujemy wzór na prawdopodobieństwo całkowite bez precyzowania jaka jest przestrzeń zdarzeń. To jest zresztą cała siła tego wzoru, że pozwala on prosto liczyć prawdopodobieństwa w sytuacjach, gdy przestrzeń zdarzeń jest dość skomplikowana. Tak jest np. w przypadku zdarzeń dwuetapowych. To jest dobre, choć nie całkiem łatwe ćwiczenie, żeby się zastanowić jaka jest przestrzeń zdarzeń w takiej sytuacji. Po odpowiedź zapraszam do kolejnych sposobów.
Sposób II
Tym razem spróbujmy nie filozofować, tylko wyliczmy żądane prawdopodobieństwo.
Zaczynamy od końca, czyli losowania pary liczb z 6 i patrzenia, czy druga jest biała. Niech 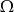 będzie zbiorem par
będzie zbiorem par 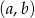 wylosowanych kul. Jakie jest prawdopodobieństwo otrzymania na drugim miejscu kuli białej? – wszystkich par jest
wylosowanych kul. Jakie jest prawdopodobieństwo otrzymania na drugim miejscu kuli białej? – wszystkich par jest 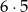 , i jeżeli w szóstce kul jest
, i jeżeli w szóstce kul jest 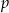 kul białych, to par z drugą kula białą jest
kul białych, to par z drugą kula białą jest 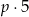 (wybieramy białą na drugie miejsce i jeszcze jedną). Zatem prawdopodobieństwo wynosi
(wybieramy białą na drugie miejsce i jeszcze jedną). Zatem prawdopodobieństwo wynosi
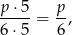
czyli dokładnie tyle, ile wylosowanie kuli białej z wszystkich sześciu.
Zatem zadanie możemy przerobić na: Przekładamy (losowo) 6 kul z pierwszej urny do drugiej. Jakie jest prawdopodobieństwo wylosowania z drugiej urny kuli białej?
Teraz radzimy sobie podobnie jak poprzednio. Niech 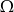 składa się z par
składa się z par 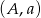 , gdzie
, gdzie 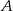 jest 6–elementowym zbiorem kul przełożonych do drugiej urny, a
jest 6–elementowym zbiorem kul przełożonych do drugiej urny, a  wylosowaną z niej kulą. W szczególności
wylosowaną z niej kulą. W szczególności 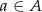 . Jak jest moc
. Jak jest moc 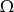 ? Podzbiór 6–elementowy możemy wybrać na
? Podzbiór 6–elementowy możemy wybrać na
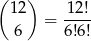
sposobów. Do tego musimy wybrać jeden z jego elementów, co nam daje
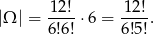
Ile jest zdarzeń sprzyjających? – białą kulę możemy wybrać na 5 sposobów. Do tego musimy dobrać 5 kul, które dadzą nam podzbiór 6–elementowy na
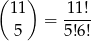
sposobów. Daje nam to prawdopodobieństwo.
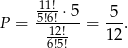
Sposób III
Mamy teraz dwie rzeczy: I sposób, który wygląda raczej nieprecyzyjnie, ale który dobrze przewiduje wynik, oraz II sposób, który jest bardzo konkretny, ale w którym w ogóle nie widać dlaczego wyszło 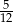 . Spróbujmy teraz te dwie rzeczy połączyć, żeby mieć jednocześnie precyzyjne rozumowanie i intuicje co się dzieje.
. Spróbujmy teraz te dwie rzeczy połączyć, żeby mieć jednocześnie precyzyjne rozumowanie i intuicje co się dzieje.
Jak już pisałem pod koniec I sposobu, w przypadku zdarzeń dwuetapowych nie jest łatwo napisać przestrzeń zdarzeń, w której stosujemy wzór na prawdopodobieństwo całkowite. W naszym zadaniu jest jeszcze gorzej, bo mamy trzy etapy, ale jak poprzednio zajmijmy się każdym z osobna.
Zastanówmy się jakie jest prawdopodobieństwo otrzymania białej kuli, jeżeli losujemy ją z wcześniej wylosowanego podzbioru 6-elementowego. Jak opisać zdarzenia elementarne? – tak jak w II sposobie: są to pary 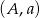 , gdzie
, gdzie 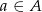 . W tym języku zdarzenia elementarne to oczywiście pary, które mają białą kulę na drugim miejscu. To co teraz jest najważniejsze, to że jest dokładnie tyle samo takich par dla każdej z kul, czyli dla każdej kuli jest dokładnie tyle samo podzbiorów 6-elementowych, które ją zawierają. To powinno być jasne, bo żadna kula nie jest wyróżniona, ale można też to łatwo policzyć: takich podzbiorów jest
. W tym języku zdarzenia elementarne to oczywiście pary, które mają białą kulę na drugim miejscu. To co teraz jest najważniejsze, to że jest dokładnie tyle samo takich par dla każdej z kul, czyli dla każdej kuli jest dokładnie tyle samo podzbiorów 6-elementowych, które ją zawierają. To powinno być jasne, bo żadna kula nie jest wyróżniona, ale można też to łatwo policzyć: takich podzbiorów jest 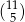 (dobieramy 5 liczb). W takim razie wszystkie zdarzenia elementarne dzielą nam się na 12 równolicznych podzbiorów, w zależności od tego, którą kulę wylosowaliśmy na końcu. Dokładnie 5 z tych podzbiorów zawiera zdarzenia sprzyjające, co nam daje żądane prawdopodobieństwo.
(dobieramy 5 liczb). W takim razie wszystkie zdarzenia elementarne dzielą nam się na 12 równolicznych podzbiorów, w zależności od tego, którą kulę wylosowaliśmy na końcu. Dokładnie 5 z tych podzbiorów zawiera zdarzenia sprzyjające, co nam daje żądane prawdopodobieństwo.
Z drugim etapem, losowania z dwóch kul, postępujemy podobnie.
Sposób IV
Można myśleć jeszcze inaczej. Powinno być jasne, że w wyniku opisanego doświadczenia, na końcu będziemy otrzymywać każdą kulę tak samo często (żadna kula nie jest wyróżniona, można też to łatwo policzyć), więc kule białe będą się pojawiać dokładnie z prawdopodobieństwem 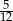 .
.
Odpowiedź: