Zadanie nr 9631511
Udowodnij, że 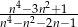 , dla
, dla 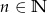 i
i 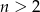 jest ułamkiem właściwym.
jest ułamkiem właściwym.
Rozwiązanie
Ułamek jest właściwy jeżeli licznik jest mniejszy od mianownika. Musimy więc wykazać nierówność
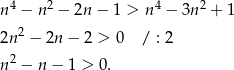
Możemy tę nierówność rozwiązać używając 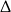 -y, ale możemy też zauważyć, że na mocy założenia
-y, ale możemy też zauważyć, że na mocy założenia 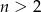 mamy
mamy