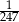Zadanie nr 9639619
Czterdzieści osób usadzono w sposób losowy przy czterech dziesięcioosobowych okrągłych stołach. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że trzy ustalone wcześniej osoby siedzą na trzech sąsiednich miejscach.
Rozwiązanie
Wszystkich możliwości usadzenia 40 osób jest
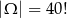
Zastanówmy się teraz na ile sposobów możemy ustalone trzy osoby posadzić obok siebie. Najpierw na 4 sposoby wybieramy stolik, przy którym będą siedzieć, potem na 10 sposobów wybieramy miejsca, na których usiądą, następnie na 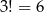 sposobów ustalamy kolejność w jakiej te osoby zajmą swoje miejsca. Na koniec, na
sposobów ustalamy kolejność w jakiej te osoby zajmą swoje miejsca. Na koniec, na 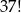 sposobów ustalamy kolejność pozostałych 37 osób. Interesujące nas prawdopodobieństwo jest więc równe
sposobów ustalamy kolejność pozostałych 37 osób. Interesujące nas prawdopodobieństwo jest więc równe
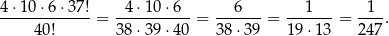
Odpowiedź: