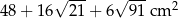/Szkoła średnia

Zadanie nr 9640595

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa jest prostokąt o bokach 6 cm i 8 cm. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod katem 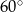60∘ . Oblicz pole powierzchni ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

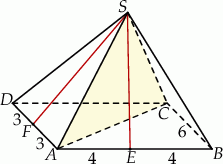
Ponieważ wszystkie krawędzie są nachylone do podstawy pod kątem 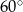60∘ , trójkąt 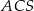ACS jest równoboczny. Długość jego boku wynosi

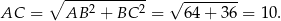
∘ ------------ √ -------- AC = AB 2 + BC 2 = 64 + 36 = 1 0.

Ściany ostrosłupa są trójkątami równoramiennymi i ich wysokości wynoszą

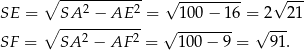
∘ ------------ √ --------- √ --- SE = SA 2 − AE 2 = 100 − 16 = 2 21 ∘ ------------ √ -------- √ --- SF = SA 2 − AF 2 = 100− 9 = 91.

Liczymy teraz pole powierzchni.

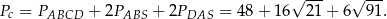
√ --- √ --- P = P + 2P + 2P = 48 + 16 21+ 6 91. c ABCD ABS DAS

 
Odpowiedź: √ --- √ --- 2 48 + 16 21+ 6 91 cm

Wersja PDF