/Szkoła średnia

Zadanie nr 9641190

Dodaj do ulubionych
Dodaj do rozwiązanych

W układzie współrzędnych narysuj okrąg o równaniu 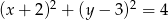2 2 (x + 2) + (y − 3) = 4 oraz zaznacz punkt 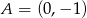A = (0,− 1) . Prosta o równaniu 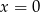x = 0 jest jedną ze stycznych do tego okręgu przechodzących przez punkt 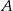A . Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt A .

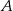Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

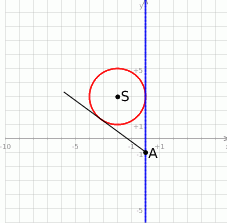
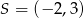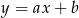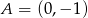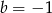Podany okrąg ma środek w punkcie S = (− 2,3) i promień 2. Szukamy prostej w postaci y = ax + b (tu jest ważne, nie szukamy pionowej prostej, bo ona jest w tej postaci). Ponieważ prosta ma przechodzić przez punkt A = (0,− 1) mamy b = − 1 , czyli szukamy prostej w postaci y = ax − 1 .

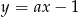Sposób I

Sprawdźmy kiedy szukana prosta i okrąg mają jeden punkt wspólny (wstawiamy 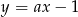y = ax− 1 ) do równania okręgu.

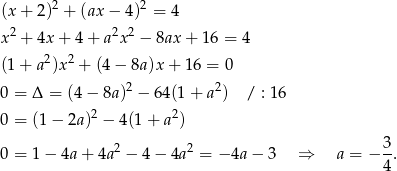
(x + 2)2 + (ax − 4)2 = 4 x2 + 4x + 4 + a2x2 − 8ax + 1 6 = 4 2 2 (1+ a )x + (4− 8a)x + 16 = 0 0 = Δ = (4 − 8a)2 − 64(1 + a2) / : 16 0 = (1 − 2a)2 − 4(1 + a2) 3 0 = 1 − 4a + 4a2 − 4 − 4a2 = − 4a − 3 ⇒ a = − --. 4

Sposób II

Szukana prosta 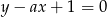y − ax + 1 = 0 będzie styczna do danego okręgu jeżeli środek tego okręgu będzie od niej odległy dokładnie o długość promienia. Korzystamy ze wzoru na odległość punktu od prostej.

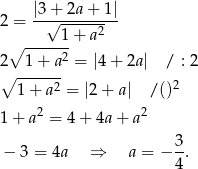
|3+--2a+--1| 2 = √ -----2 ∘ -----1+ a 2 1 + a2 = |4+ 2a| / : 2 ∘ ------ 2 1+ a2 = |2+ a| /() 1 + a2 = 4+ 4a+ a2 3- − 3 = 4a ⇒ a = − 4 .

 
Odpowiedź: y = − 3x− 1 4

Wersja PDF