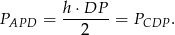Zadanie nr 9648299
Na przekątnej 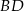 równoległoboku
równoległoboku 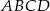 obrano dowolny punkt
obrano dowolny punkt 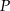 . Wykaż, że pola trójkątów
. Wykaż, że pola trójkątów 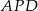 i
i 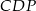 są równe.
są równe.
Rozwiązanie
Zaczynamy od rysunku
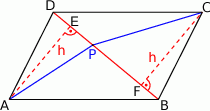
Zauważmy, że przekątna 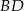 dzieli równoległobok na dwa przystające trójkąty
dzieli równoległobok na dwa przystające trójkąty 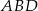 i
i 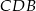 . W szczególności wysokości opuszczone z wierzchołków
. W szczególności wysokości opuszczone z wierzchołków 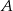 i
i 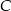 w tych trójkątach mają równe długości. To jednak oznacza, że
w tych trójkątach mają równe długości. To jednak oznacza, że