Zadanie nr 9656817
Czy istnieje taki wielokąt, który ma 2 razy więcej przekątnych niż boków?
Rozwiązanie
Sposób I
Ponieważ w wielokącie z każdego wierzchołka wychodzi tyle samo przekątnych, w wielokącie spełniającym warunki zadania z każdego wierzchołka muszą wychodzić 4 przekątne (dwa razy więcej niż boków). Zatem wielokąt musi mieć 7 wierzchołków (końce 4 przekątnych, plus wierzchołek, na który patrzymy i jego dwaj sąsiedzi). Łatwo sprawdzić, że 7–kąt rzeczywiście ma 14 przekątnych.
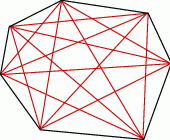
Sposób II
Możemy skorzystać ze wzoru
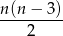
na liczbę przekątnych  –kąta. Wzór ten jest wyprowadzony tu. Wzór ten daje nam równanie
–kąta. Wzór ten jest wyprowadzony tu. Wzór ten daje nam równanie
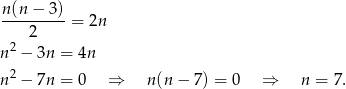
Odpowiedź: Siedmiokąt

