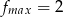/Szkoła średnia

Zadanie nr 9661658

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź najmniejszą i największą wartość funkcji 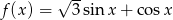√ -- f(x) = 3sinx + co sx w przedziale ⟨0 ;2π⟩ .

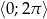Rozwiązanie

Skorzystamy ze wzoru

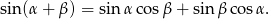
sin (α+ β) = sinα cos β+ sin β cos α.

Przekształcamy podany wzór funkcji

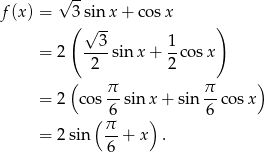
√ -- f(x) = 3sinx + co sx ( √ -- ) = 2 --3-sinx + 1co sx 2 2 ( π π ) = 2 co s-- sin x + sin --cosx ( π6 ) 6 = 2sin --+ x . 6

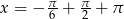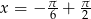Jest teraz jasne, że najmniejsza i największa wartośc to -2 i 2 odpowiednio. Wartości te są osiągane w punktach x = − π6 + π2-+ π i x = − π6 + π2- .

Zadanie można też rozwiązać licząc ekstrema podanej funkcji (przy pomocy pochodnej).  
Odpowiedź: 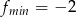fmin = − 2 i fmax = 2

Wersja PDF