Zadanie nr 9665110
Miary kątów trójkąta prostokątnego tworzą ciąg arytmetyczny. Jeśli trójkąt ten będziemy obracać wokół dłuższej przyprostokątnej, to otrzymamy stożek, którego pole powierzchni bocznej wynosi 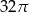 . Oblicz długości boków tego trójkąta.
. Oblicz długości boków tego trójkąta.
Rozwiązanie
Zaczynamy od rysunku
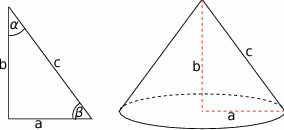
Wiemy, że liczby 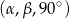 tworzą ciąg arytmetyczny (ciąg arytmetyczny jest zawsze monotoniczny, więc jest to jedna z dwóch możliwych kolejności miar kątów, druga to:
tworzą ciąg arytmetyczny (ciąg arytmetyczny jest zawsze monotoniczny, więc jest to jedna z dwóch możliwych kolejności miar kątów, druga to: 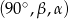 ; ta druga możliwość prowadzi jednak do tego samego wyniku).
; ta druga możliwość prowadzi jednak do tego samego wyniku).
Ponieważ 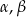 są kątami ostrymi w trójkącie prostokątnym, więc
są kątami ostrymi w trójkącie prostokątnym, więc 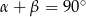 . W ciągu arytmetycznym, wyraz środkowy jest średnią arytmetyczną wyrazów sąsiednich, więc
. W ciągu arytmetycznym, wyraz środkowy jest średnią arytmetyczną wyrazów sąsiednich, więc
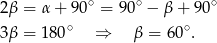
Stąd 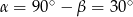 oraz
oraz
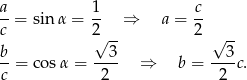
Wykorzystujemy informację o polu powierzchni bocznej.
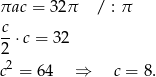
Stąd
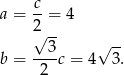
Odpowiedź: