Zadanie nr 9665554
Suma długości wszystkich wysokości trójkąta 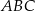 jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt
jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt 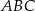 jest równoboczny.
jest równoboczny.
Rozwiązanie
Szkicujemy trójkąt.
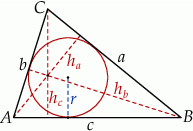
Przyjmijmy oznaczenia jak na rysunku, tzn. niech 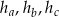 będą wysokościami opuszczonymi odpowiednio na boki o długościach:
będą wysokościami opuszczonymi odpowiednio na boki o długościach: 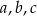 . Mamy zatem
. Mamy zatem
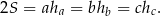
Ponadto, jeżeli przez  oznaczymy promień okręgu wpisanego w trójkąt
oznaczymy promień okręgu wpisanego w trójkąt 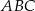 , to
, to
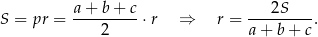
Mamy zatem
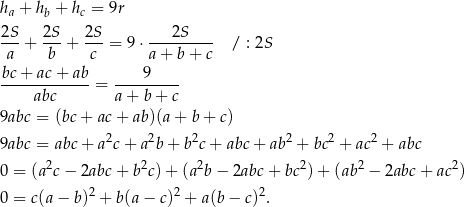
Ponieważ liczby 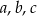 są dodatnie, otrzymana równość zachodzi wtedy i tylko wtedy, gdy
są dodatnie, otrzymana równość zachodzi wtedy i tylko wtedy, gdy
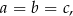
czyli gdy trójkąt 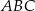 jest równoboczny.
jest równoboczny.

