Zadanie nr 9671439
Na bokach 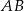 i
i 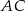 trójkąta
trójkąta 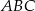 , który nie jest równoramienny, wybrano takie punkty
, który nie jest równoramienny, wybrano takie punkty 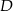 i
i 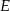 , że
, że 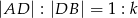 oraz
oraz 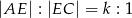 , dla
, dla 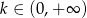 .
.
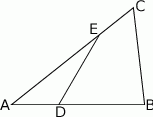
- Wyznacz wzór funkcji
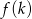 , która jest zdefiniowana jako stosunek pól trójkątów
, która jest zdefiniowana jako stosunek pól trójkątów 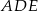 i
i 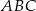 .
. - Wiedząc że
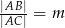 , dla
, dla 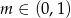 wyznacz wszystkie wartości parametru
wyznacz wszystkie wartości parametru 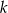 , dla których trójkąty
, dla których trójkąty 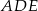 i
i 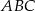 są podobne.
są podobne.
Rozwiązanie
-
Sposób I
Jeżeli dorysujemy wysokości opuszczone z punktów
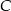 i
i 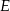 na bok
na bok 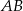 ,
, 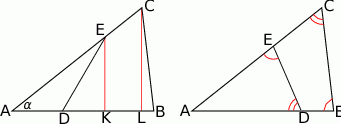
to z podobieństwa trójkątów
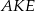 i
i 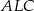 mamy
mamy 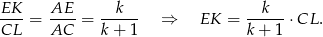
Ponadto z założenia
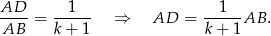
Możemy więc wyliczyć pole trójkąta
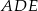 w zależności od pole trójkąta
w zależności od pole trójkąta 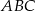 .
. 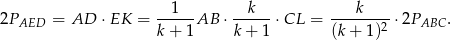
Zatem
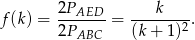
Sposób II
Szukany stosunek pól można też łatwo wyliczyć ze wzoru na pole z sinusem.
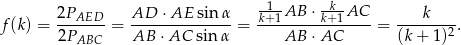
Odpowiedź: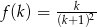
- Ponieważ trójkąt
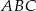 nie jest równoramienny oraz ma on wspólny kąt
nie jest równoramienny oraz ma on wspólny kąt 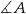 z trójkątem
z trójkątem 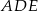 , mamy dokładnie dwie możliwości: albo
, mamy dokładnie dwie możliwości: albo 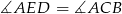 albo
albo 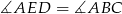 .
. W pierwszej sytuacji proste
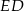 i
i 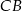 są równoległe co oznacza, że
są równoległe co oznacza, że 
W drugiej sytuacji, z podobieństwa trójkątów
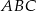 i
i 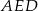 mamy
mamy 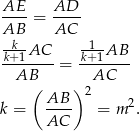
Odpowiedź: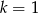 lub
lub