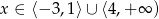Zadanie nr 9677349
Wielomian 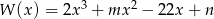 jest podzielny przez każdy z dwumianów
jest podzielny przez każdy z dwumianów 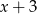 i
i 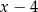 . Oblicz wartości współczynników
. Oblicz wartości współczynników  i
i 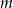 oraz rozwiąż nierówność
oraz rozwiąż nierówność 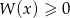 .
.
Rozwiązanie
Jeżeli wielomian 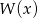 dzieli się przez
dzieli się przez 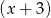 i przez
i przez 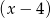 , to
, to 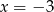 i
i 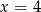 są jego pierwiastkami. Mamy więc
są jego pierwiastkami. Mamy więc
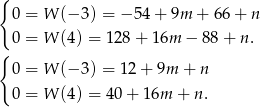
Odejmujemy od drugiego równania pierwsze (żeby skrócić  ) i mamy
) i mamy
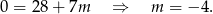
Z pierwszego równania układu otrzymujemy
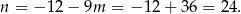
Stąd
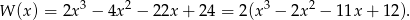
Wiemy, że 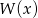 dzieli się przez
dzieli się przez
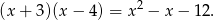
Wykonujemy to dzielenie – my zrobimy to grupując wyrazy.
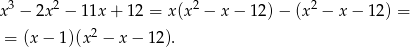
Pozostało rozwiązać nierówność
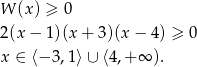
Odpowiedź: 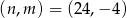 ,
,