Zadanie nr 9682450
Czy kąt zewnętrzny wielokąta foremnego może mieć miarę 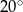 ?
?
Rozwiązanie
Sposób I
Wiadomo, że suma kątów zewnętrznych w dowolnym wielokącie wynosi 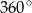 . Zatem w
. Zatem w  –kącie foremnym kąt zewnętrzny ma miarę
–kącie foremnym kąt zewnętrzny ma miarę 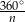 . Daje to nam równanie
. Daje to nam równanie
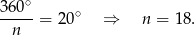
Sposób II
Wiadomo, że suma kątów wewnętrznych dowolnego  –kąta wypukłego (a tak naprawdę dowolnego) wynosi
–kąta wypukłego (a tak naprawdę dowolnego) wynosi 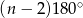 . Zatem kąt wewnętrzny w
. Zatem kąt wewnętrzny w  –kącie foremnym jest równy
–kącie foremnym jest równy 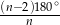 . Daje to nam równanie
. Daje to nam równanie
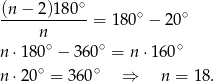
Odpowiedź: Tak, w osiemnastokącie foremnym

