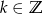Zadanie nr 9685582
Wyznacz wszystkie liczby rzeczywiste  , spełniające równanie
, spełniające równanie
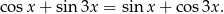
Rozwiązanie
Korzystamy ze wzorów na różnicę sinusów i różnicę cosinusów.
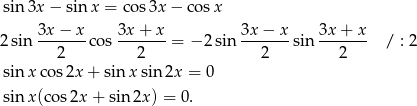
Otrzymujemy stąd 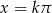 lub
lub
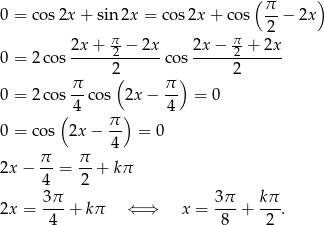
Odpowiedź: 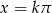 lub
lub 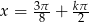 ,
, 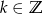
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie liczby rzeczywiste  , spełniające równanie
, spełniające równanie
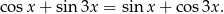
Korzystamy ze wzorów na różnicę sinusów i różnicę cosinusów.
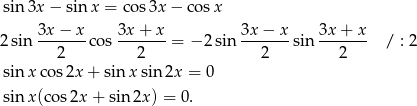
Otrzymujemy stąd 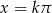 lub
lub
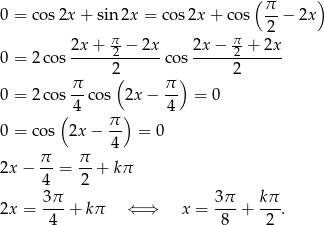
Odpowiedź: 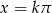 lub
lub 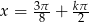 ,
,