Zadanie nr 9708961
Dany jest romb, którego kąt ostry ma miarę 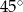 , a jego pole jest równe
, a jego pole jest równe 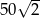 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Rozwiązanie
Zaczynamy od rysunku.
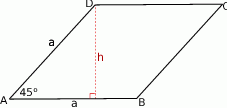
Jeżeli oznaczymy przez  długość boku rombu to ze wzoru na pole równoległoboku z sinusem, mamy
długość boku rombu to ze wzoru na pole równoległoboku z sinusem, mamy
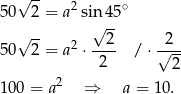
Aby obliczyć długość wysokości 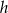 raz jeszcze korzystamy z podanego pola
raz jeszcze korzystamy z podanego pola
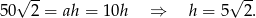
Sposób II
Zauważmy, że
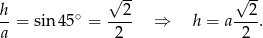
Ponadto z podanego pola
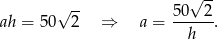
Podstawiając to wyrażenie w poprzedniej równości mamy
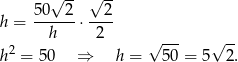
Odpowiedź: