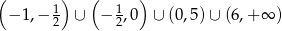/Szkoła średnia

Zadanie nr 9710906

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę funkcji

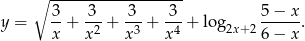
∘ ------------------- y = 3-+ 3--+ -3-+ 3-+ lo g 5−--x. x x2 x3 x4 2x+2 6− x

Rozwiązanie

Ponieważ x jest w mianowniku, musimy mieć x ⁄= 0 .

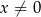Sposób I

Spróbujmy na początek ustalić kiedy wyrażenie pod pierwiastkiem jest nieujemne.

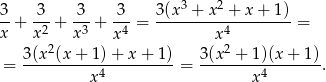
3 3 3 3 3(x 3 + x 2 + x + 1) --+ --2 + -3-+ ---= -------------------= x x x x 4 x4 3(x2(x-+-1-)+-x-+-1)- 3(x-2 +-1)(x-+-1-) = x4 = x4 .

Widać, że wyrażenie to jest nieujemne dla 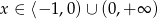x ∈ ⟨− 1,0) ∪ (0,+ ∞ ) .

Zajmijmy się teraz logarytmem. Podstawa logarytmu musi być dodatnia, czyli 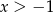x > − 1 oraz musi być różna od 1, czyli 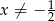1 x ⁄= − 2 . Ponadto, argument logarytmu musi być dodatni, czyli

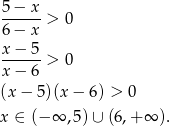
5− x ------> 0 6− x x−--5- x− 6 > 0 (x − 5 )(x − 6) > 0 x ∈ (−∞ ,5 )∪ (6,+ ∞ ).

Zbierając wszystkie warunki razem mamy dziedzinę

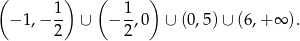
( 1 ) ( 1 ) − 1,− -- ∪ − -,0 ∪ (0 ,5 )∪ (6,+ ∞ ). 2 2

Sposób II

Tym razem zauważmy, że pod pierwiastkiem mamy sumę czterech pierwszych wyrazów ciągu geometrycznego o ilorazie 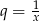1 q = x . Widać, że 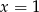x = 1 należy do dziedziny funkcji, a jeżeli 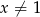x ⁄= 1 to możemy skorzystać ze wzoru na sumę początkowych wyrazów ciągu geometrycznego.

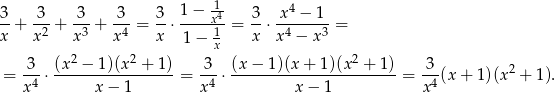
3 3 3 3 3 1− 1x4 3 x 4 − 1 --+ -2 + -3-+ -4-= --⋅ ----1--= --⋅ -4----3-= x x x x x 1 − x x x − x 3 (x 2 − 1 )(x2 + 1) 3 (x− 1)(x + 1)(x2 + 1) 3 2 = -4-⋅ -----------------= --4 ⋅-----------------------= -4(x + 1)(x + 1). x x − 1 x x − 1 x

Widać teraz, że wyrażenie pod pierwiastkiem jest nieujemne dla 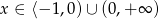x ∈ ⟨− 1,0 )∪ (0,+ ∞ ) . Dalej postępujemy tak samo jak w pierwszym sposobie.  
Odpowiedź: ( ) ( ) − 1,− 12 ∪ − 12,0 ∪ (0,5)∪ (6 ,+∞ )

Wersja PDF