/Szkoła średnia

Zadanie nr 9714474

Dodaj do ulubionych
Dodaj do rozwiązanych

Na poniższym rysunku przedstawiono łamaną 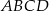ABCD , która jest wykresem funkcji y = f(x ) .

PIC

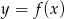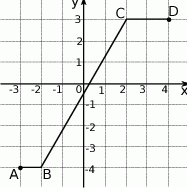
Korzystając z tego wykresu

  • zapisz w postaci przedziału zbiór wartości funkcji f ,
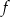  • podaj wartość funkcji 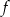f dla argumentu x = 1− √ 10- ,
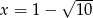  • wyznacz równanie prostej BC ,
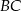  • oblicz długość odcinka BC .

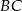Rozwiązanie

  • Odczytujemy z wykresu.  
    Odpowiedź: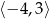 ⟨− 4,3⟩
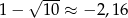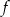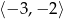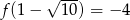  • Ponieważ √ --- 1 − 10 ≈ − 2,16 oraz funkcja f jest stała na przedziale ⟨− 3,− 2⟩ , to √ --- f(1 − 10) = − 4 .  
    Odpowiedź: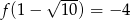 √ --- f(1 − 10) = − 4
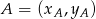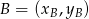  • Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA,yA ) i B = (xB,yB ) :
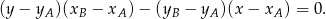
    (y − yA )(xB − xA )− (yB − yA)(x − xA ) = 0.

    W naszej sytuacji

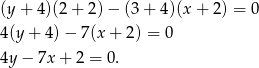
    (y+ 4)(2+ 2)− (3+ 4)(x+ 2) = 0 4(y + 4) − 7(x + 2) = 0 4y − 7x + 2 = 0 .

     
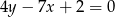
    Odpowiedź: 4y− 7x + 2 = 0

  • Liczymy
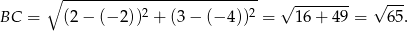
    ∘ --------------------------- √ -------- √ --- BC = (2 − (− 2))2 + (3 − (− 4))2 = 16 + 49 = 65.

     
    Odpowiedź: √ --- 65

Wersja PDF