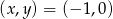Zadanie nr 9716185
Rozwiąż graficznie i algebraicznie układ równań
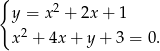
Rozwiązanie
Aby podany układ rozwiązać graficznie, napiszmy go w postaci
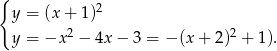
Rysujemy teraz wykresy obu funkcji i szukamy ich punktów przecięcia.
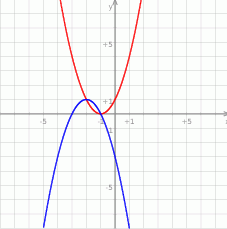
Widać z wykresu, że są to punkty 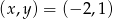 lub
lub 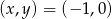 .
.
Rozwiążmy teraz ten układ algebraicznie (porównujemy 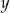 -ki).
-ki).
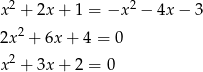
Dalej, 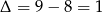 ,
, 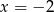 lub
lub 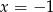 . Stąd
. Stąd 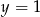 lub
lub 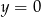 .
.
Odpowiedź: 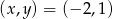 lub
lub