/Szkoła średnia

Zadanie nr 9725499

Dodaj do ulubionych
Dodaj do rozwiązanych

O pewnym ciągu arytmetycznym wiadomo, że ma dziesięć wyrazów. Suma jego wyrazów o numerach nieparzystych jest równa 75, a suma wyrazów o numerach parzystych jest równa 90. Wyznacz pierwszy wyraz tego ciągu.

Rozwiązanie

Ponieważ

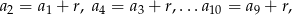
a2 = a1 + r, a4 = a3 + r,...a 10 = a9 + r,

mamy

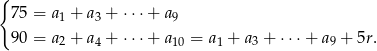
{ 75 = a1 + a3 + ⋅⋅⋅+ a9 90 = a2 + a4 + ⋅⋅⋅+ a10 = a1 + a3 + ⋅⋅⋅+ a9 + 5r.

Odejmując od pierwszego równania drugie, mamy

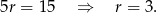
5r = 1 5 ⇒ r = 3.

Zauważmy teraz, że suma wszystkich 10 wyrazów jest równa 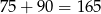75+ 90 = 165 , co daje nam równanie

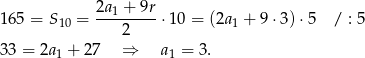
2a1 + 9r 165 = S10 = ---------⋅10 = (2a1 + 9⋅3) ⋅5 / : 5 2 33 = 2a 1 + 2 7 ⇒ a1 = 3.

 
Odpowiedź: a1 = 3

Wersja PDF