/Szkoła średnia

Zadanie nr 9731774

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że ciąg określony wzorem 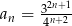32n+-1 an = 4n+2 jest ciągiem geometrycznym. Wyznacz iloraz osiemnastego wyrazu tego ciągu przez wyraz 16.

Rozwiązanie

Musimy pokazać, że iloraz dwóch kolejnych wyrazów ciągu jest stały (nie zależy od n ). Liczymy

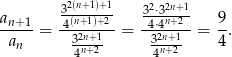
2(n+ 1)+1 2 2n+1 an+ 1 34(n+1)+-2- 34⋅⋅34n+2- 9 ----- = --32n+1-- = -32n+1--= -. an 4n+2 4n+2 4

Zatem ciąg jest ciągiem geometrycznym o ilorazie 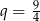q = 94 .

Iloraz osiemnastego i szesnastego wyrazu ciągu jest równy

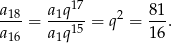
a18 a1q17 2 81- a = a q15 = q = 16. 16 1

 
Odpowiedź: 81 16

Wersja PDF