Zadanie nr 9737560
W równoległoboku 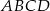 , w którym
, w którym 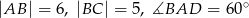 poprowadzono wysokości
poprowadzono wysokości 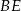 i
i 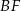 na boki
na boki 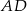 i
i 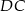 .
.
- Wykonaj odpowiedni rysunek i oblicz długości odcinków
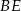 i
i 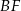 .
. - Oblicz pole trójkąta
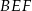 .
.
Rozwiązanie
- Zaczynamy oczywiście od rysunku.
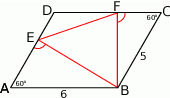
Sposób I
Ze wzoru na pole równoległobok z sinusem możemy policzyć pole równoległoboku
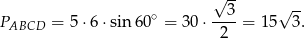
Z drugiej strony, pole to iloczyn podstawy i wysokości, czyli
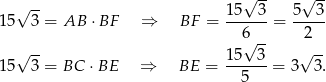
Sposób II
Z trójkątów prostokątnych
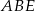 i
i 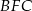 mamy
mamy 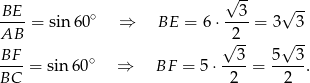
Odpowiedź: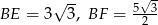
- Zauważmy, że
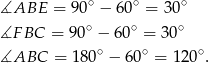
Zatem
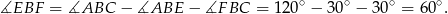
Zatem znamy długości dwóch boków trójkąta
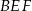 oraz kąt między nimi. Możemy więc policzyć jego pole ze wzoru z sinusem.
oraz kąt między nimi. Możemy więc policzyć jego pole ze wzoru z sinusem. 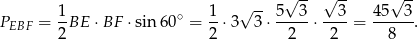
Odpowiedź: