Zadanie nr 9742387

Funkcja 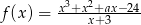x3+x-2+ax−24- f(x) = x+3 ma miejsce zerowe równe (-2). Wyznacz:

Rozwiązanie

Wstawiamy 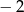i sprawdzamy kiedy (dla jakiego ) wychodzi 0.
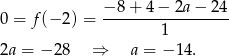
$0 = f(− 2 ) = −-8+--4−--2a−--24- 1 2a = − 28 ⇒ a = − 14.$

Odpowiedź: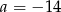
Oczywiście wystarczy zajmować się licznikiem podanego ułamka. Dzielimy go przez dwumian 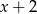. My zrobimy to grupując wyrazy.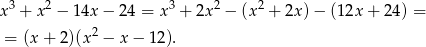
$x 3 + x 2 − 1 4x− 24 = x3 + 2x 2 − (x 2 + 2x )− (12x + 24) = 2 = (x+ 2)(x − x− 12).$

Pozostało rozłożyć trójmian w nawiasie.

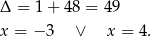
$Δ = 1 + 48 = 4 9 x = − 3 ∨ x = 4.$

Jednak 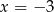to dokładnie miejsce zerowe mianownika, więc pozostaje .
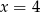Odpowiedź: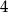
Musimy rozwiązać nierówność.
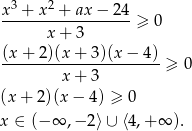
$3 2 x-+--x-+--ax-−-24-≥ 0 x + 3 (x+ 2)(x + 3)(x − 4) ----------------------≥ 0 x + 3 (x + 2 )(x− 4) ≥ 0 x ∈ (− ∞ ,− 2 ⟩∪ ⟨4,+ ∞ ).$

Trzeba jeszcze pamiętać o wyrzuceniu z tego zbioru miejsca zerowego mianownika, czyli .
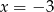Odpowiedź: