Zadanie nr 9747002
W trapezie równoramiennym, który nie jest równoległobokiem, ramię ma długość 7 cm, a przekątna 8 cm. Oblicz długości podstaw trapezu wiedząc, że odcinek łączący środki ramion trapezu ma długość 4 cm.
Rozwiązanie
Zaczynamy od rysunku i obserwacji, że odcinek łączący środki ramion w trapezie o podstawach  i
i 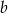 ma długość
ma długość 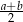 – łatwo to odczytać z prawego rysunku.
– łatwo to odczytać z prawego rysunku.
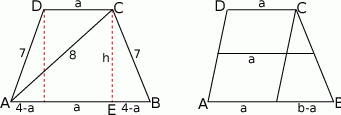
Zatem suma podstaw trapezu wynosi 8 i jeżeli oznaczymy 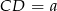 to
to 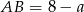 oraz
oraz
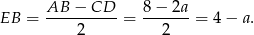
Sposób I
Zauważmy, że 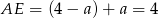 , zatem stosując twierdzenie Pitagorasa w trójkącie
, zatem stosując twierdzenie Pitagorasa w trójkącie 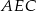 mamy
mamy
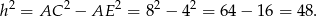
Patrzymy teraz na trójkąt  .
.
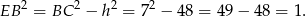
Zatem 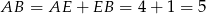 i
i 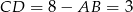 .
.
Sposób II
Stosując twierdzenie Pitagorasa w każdym z trójkątów 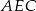 i
i 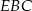 mamy
mamy
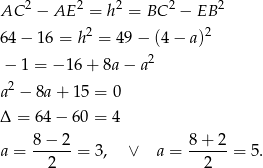
Przy naszych oznaczeniach musi być 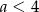 , więc
, więc 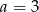 , a
, a 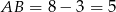 .
.
Odpowiedź: 3 i 5

