/Szkoła średnia

Zadanie nr 9755249

Dodaj do ulubionych
Dodaj do rozwiązanych

Na trapezie opisano okrąg o średnicy długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc, że przekątna tego trapezu ma długość 20 cm, oblicz pole tego trapezu.

Rozwiązanie

Narysujmy opisaną sytuację.

PIC

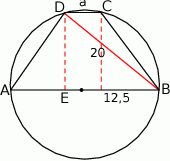
Ponieważ podstawa 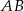AB jest średnicą okręgu, trójkąt 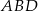ABD jest prostokątny, skąd

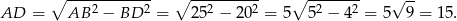
∘ ------------ ∘ ---------- ∘ ------- √ -- AD = AB 2 − BD 2 = 252 − 202 = 5 52 − 42 = 5 9 = 1 5.

Obliczmy teraz wysokość 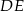DE trójkąta 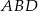ABD (a więc również wysokość trapezu). Porównujemy dwa wzory na pole (inny sposób to wykorzystać podobieństwo trójkątów 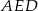AED i ADB ).

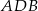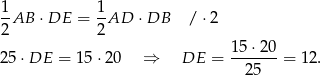
1-AB ⋅DE = 1-AD ⋅DB / ⋅2 2 2 15⋅2-0- 25 ⋅DE = 1 5⋅20 ⇒ DE = 2 5 = 12.

Pozostało jeszcze obliczyć długość 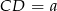CD = a drugiej postawy trapezu. Z trójkąta prostokątnego 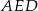AED mamy

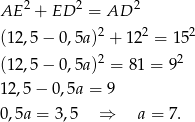
AE 2 + ED 2 = AD 2 (12,5− 0,5a)2 + 122 = 152 2 2 (12,5− 0,5a) = 81 = 9 12,5− 0,5a = 9 0,5a = 3,5 ⇒ a = 7.

Zatem pole trapezu jest równe

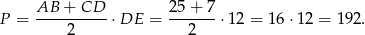
AB + CD 25 + 7 P = ----------⋅DE = -------⋅12 = 16⋅ 12 = 192. 2 2

 
Odpowiedź: 192 cm 2

Wersja PDF