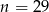Zadanie nr 9755507
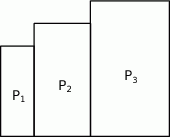
Niech 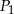 będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty
będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty 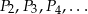 w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
Wyznacz liczbę  , dla której obwód prostokąta
, dla której obwód prostokąta 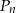 jest równy 246.
jest równy 246.
Rozwiązanie
Jeżeli przez 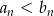 oznaczymy długości boków prostokąta o numerze
oznaczymy długości boków prostokąta o numerze  , to
, to 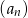 i
i 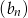 są ciągami arytmetycznymi o różnicy
są ciągami arytmetycznymi o różnicy 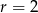 . Zatem
. Zatem
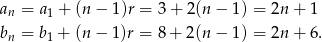
Musimy więc rozwiązać równanie
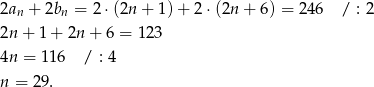
Odpowiedź: