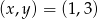Zadanie nr 9756123
Rozwiąż układ równań 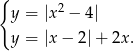
Rozwiązanie
Patrząc na znaki wyrażeń 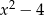 i
i 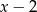 , mamy 3 możliwości
, mamy 3 możliwości
Jeżeli 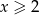 , to mamy układ równań
, to mamy układ równań
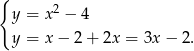
Porównując 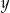 –ki mamy
–ki mamy
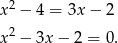
Dalej, 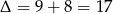 ,
, 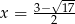 lub
lub 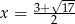 . Tylko druga z tych liczb spełnia założenie
. Tylko druga z tych liczb spełnia założenie 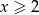 , wtedy
, wtedy
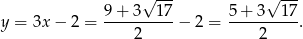
Jeżeli 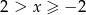 to mamy układ równań
to mamy układ równań
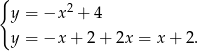
Porównując 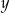 –ki mamy
–ki mamy
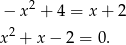
Dalej, 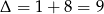 ,
, 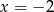 lub
lub 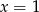 . Mamy wtedy
. Mamy wtedy 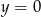 lub
lub 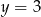 odpowiednio.
odpowiednio.
Jeżeli 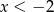 to mamy układ równań
to mamy układ równań
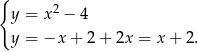
Porównując 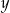 –ki mamy
–ki mamy
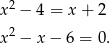
Dalej 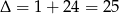 ,
, 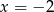 lub
lub 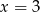 . Żadna z tych liczb nie spełnia warunku
. Żadna z tych liczb nie spełnia warunku 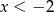 .
.
Odpowiedź: 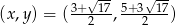 lub
lub 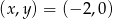 lub
lub