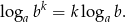Zadanie nr 9762574
Udowodnij, że liczby 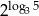 i
i 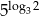 są równe.
są równe.
Rozwiązanie
Sprawdźmy
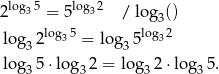
Otrzymana równość jest oczywiście prawdziwa, a przekształcaliśmy w sposób równoważny, więc wyjściowa równość też musiała być prawdziwa. Po drodze skorzystaliśmy ze wzoru
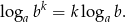
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że liczby 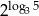 i
i 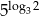 są równe.
są równe.
Sprawdźmy
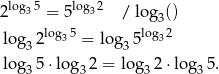
Otrzymana równość jest oczywiście prawdziwa, a przekształcaliśmy w sposób równoważny, więc wyjściowa równość też musiała być prawdziwa. Po drodze skorzystaliśmy ze wzoru