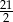/Szkoła średnia

Zadanie nr 9762890

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trapez opisany na okręgu, którego kąty przy jednej podstawie są ostre, oraz którego pole jest równe 168. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów jeżeli ramiona trapezu mają długości 13 i 15.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

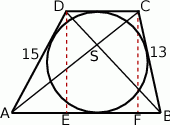
Ponieważ trapez jest opisany na okręgu, to

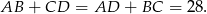
AB + CD = AD + BC = 28 .

Ponieważ znamy pole, możemy wyliczyć wysokość trapezu.

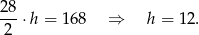
2 8 ---⋅ h = 168 ⇒ h = 12. 2

Mamy stąd

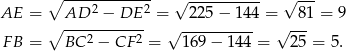
∘ ----2------2 √ ---------- √ --- AE = ∘ AD---−--DE- = 225 − 1 44 = 81 = 9 FB = BC 2 − CF 2 = √ 169-−-1-44 = √ 25-= 5 .

Jeżeli teraz a jest długością górnej podstawy, to

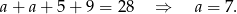
a+ a+ 5+ 9 = 28 ⇒ a = 7.

Podstawy mają więc długości 7 i 21.

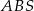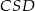Trójkąty ABS i CSD są podobne w skali 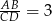AB CD-= 3 . Zatem wysokość trójkąta 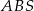ABS opuszczona z wierzchołka 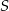S jest równa 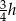3h 4 , stąd

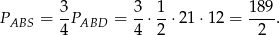
3 3 1 189 PABS = -PABD = --⋅--⋅21 ⋅12 = ----. 4 4 2 2

Stąd

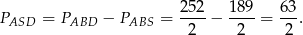
252 189 63 PASD = PABD − PABS = -2--− -2--= 2-.

Jak już zauważyliśmy trójkąt 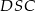DSC jest 3 razy mniejszy od trójkąta 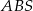ABS , zatem

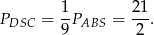
1 2 1 PDSC = 9PABS = -2-.

Ponadto

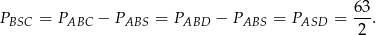
63- PBSC = PABC − PABS = PABD − PABS = PASD = 2 .

 
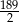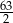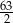Odpowiedź: 189 2 , 63- 2 , 63 2 , 21- 2

Wersja PDF