Zadanie nr 9765042
Rysunek przedstawia siatkę ostrosłupa prostego o podstawie będącej prostokątem.
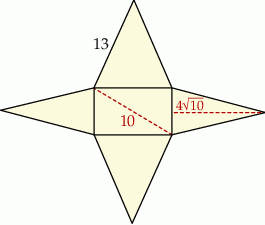
Objętość tego ostrosłupa jest równa
A) 192 B) 96 C) 576 D) 384
Rozwiązanie
Wszystkie krawędzie boczne ostrosłupa mają oczywiście długość 13.
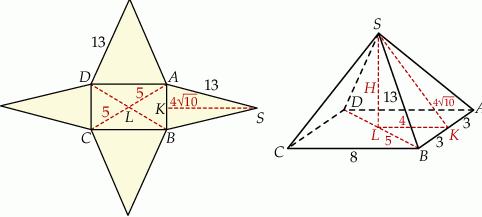
Z trójkąta prostokątnego  mamy
mamy
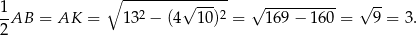
Zatem 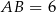 i
i
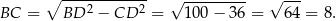
Wysokość ostrosłupa możemy obliczyć z trójkąta prostokątnego  lub
lub  . My liczymy z tego drugiego trójkąta.
. My liczymy z tego drugiego trójkąta.
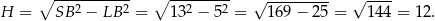
Objętość ostrosłupa jest więc równa
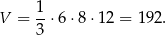
Odpowiedź: A

