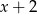/Szkoła średnia

Zadanie nr 9765655

Dodaj do ulubionych
Dodaj do rozwiązanych

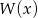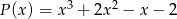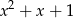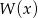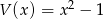Reszta z dzielenia wielomianu W (x) przez wielomian 3 2 P (x) = x + 2x − x − 2 jest równa x2 + x + 1 . Wyznacz resztę z dzielenia wielomianu W (x ) przez wielomian V(x ) = x2 − 1 .

Rozwiązanie

Sposób I

Wiemy, że

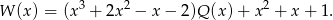
3 2 2 W (x ) = (x + 2x − x − 2)Q (x) + x + x + 1.

Oznaczmy szukanę resztę przez 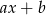ax + b , tzn.

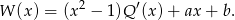
2 ′ W (x) = (x − 1)Q (x) + ax + b.

(jeżeli ktoś nie wie dlaczego jest liniowa, to niech zajrzy do poradnika).

Mamy zatem

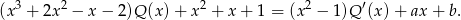
(x 3 + 2x 2 − x− 2)Q (x)+ x2 + x+ 1 = (x2 − 1)Q ′(x)+ ax+ b.

Wstawiamy teraz w tej równości x = − 1 i x = 1 (miejsca zerowe x 2 − 1 ).

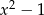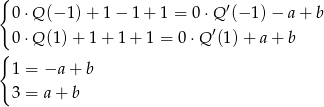
{ ′ 0⋅Q (− 1) + 1 − 1+ 1 = 0 ⋅Q (− 1) − a + b 0⋅Q (1) + 1 + 1 + 1 = 0 ⋅Q ′(1 )+ a + b { 1 = −a + b 3 = a+ b

Dodając równania stronami mamy 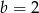b = 2 , zatem a = 1 .

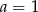Sposób II

Zauważmy, że

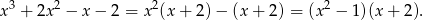
x3 + 2x2 − x − 2 = x2(x+ 2)− (x+ 2) = (x2 − 1)(x + 2).

Wiemy zatem, że

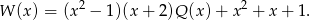
W (x) = (x 2 − 1)(x + 2 )Q(x )+ x 2 + x+ 1.

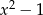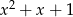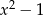To oznacza, że reszta z dzielenia tego wielomianu przez x2 − 1 jest taka sama jak reszta z dzielenia wielomianu x 2 + x + 1 przez x2 − 1 . Wykonujemy to dzielenie (grupując wyrazy).

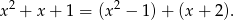
2 2 x + x + 1 = (x − 1) + (x + 2).

Szukana reszta jest więc równa 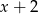x+ 2 .  
Odpowiedź: x + 2

Wersja PDF