Zadanie nr 9766220
Wielomian 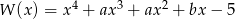 jest podzielny przez wielomian
jest podzielny przez wielomian 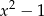 . Wynika stąd, że
. Wynika stąd, że
A) 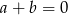 B)
B) 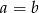 C)
C) 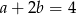 D)
D) 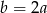
Rozwiązanie
Ponieważ 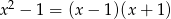 , wystarczy sprawdzić, kiedy wielomian
, wystarczy sprawdzić, kiedy wielomian 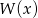 jest podzielny przez
jest podzielny przez 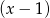 i
i 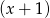 .
.
Wielomian 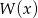 jest podzielny przez dwumian
jest podzielny przez dwumian 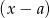 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 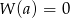 (aby się o tym przekonać wystarczy podstawić
(aby się o tym przekonać wystarczy podstawić  w równości
w równości 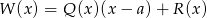 ).
).
W naszej sytuacji mamy więc
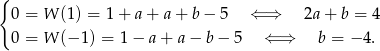
Z pierwszego równania mamy więc 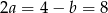 , czyli
, czyli 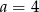 . Stąd
. Stąd  .
.
Odpowiedź: A

