Zadanie nr 9769323
W graniastosłupie prawidłowym sześciokątnym krawędź boczna jest dwa razy dłuższa od krawędzi podstawy. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
Rozwiązanie
Zaczynamy od rysunku i oznaczmy długość krawędzi graniastosłupa przez 
.
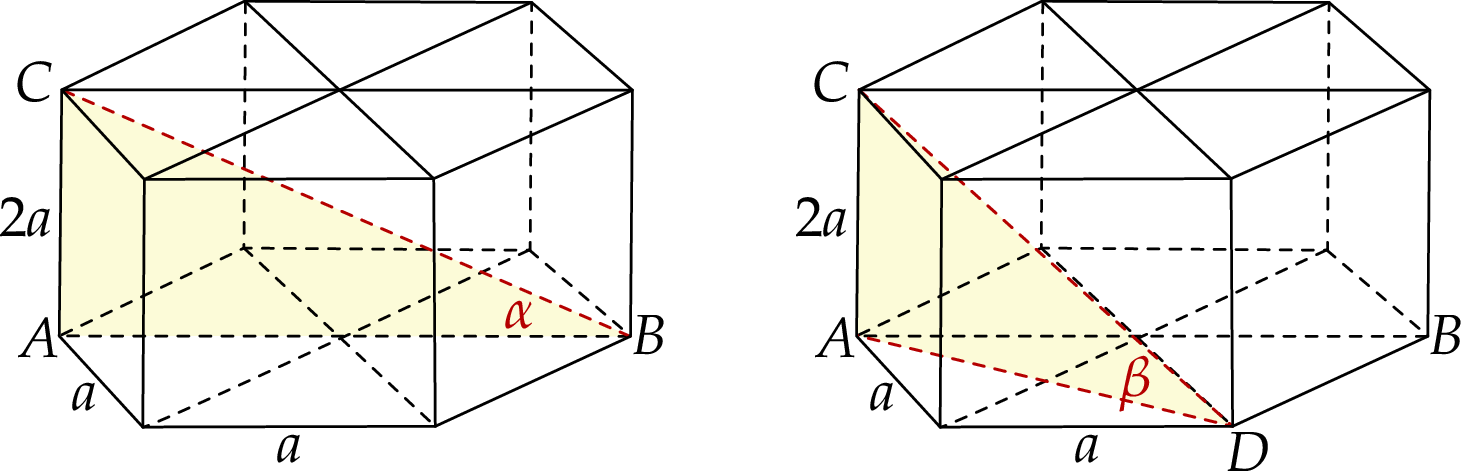
Widać, że w graniastosłupie są dwa rodzaje przekątnych takie jak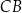 
i takie jak 
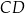. Ponieważ łącząc wierzchołki sześciokąta foremnego z jego środkiem otrzymujemy 6 trójkątów równobocznych, mamy
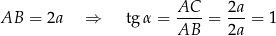
Aby wyliczyć tangens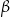 
zauważmy, że odcinek 
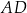jest dwa razy dłuższy od wysokości trójkąta równobocznego o boku 
, ma więc długość
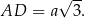
Zatem
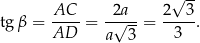
Odpowiedź: 1 i 
