/Szkoła średnia

Zadanie nr 9778540

Dodaj do ulubionych
Dodaj do rozwiązanych

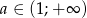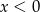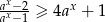Wykaż, że jeśli a ∈ (1;+ ∞ ) i x < 0 to prawdziwa jest nierówność x aax−−-21 ≥ 4ax + 1 .

Rozwiązanie

Przy podanych założeniach mamy 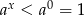x 0 a < a = 1 (funkcja 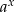x a jest rosnąca). Podstawmy 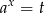ax = t , mamy wtedy 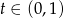t ∈ (0,1) . Przekształćmy podaną nierówność

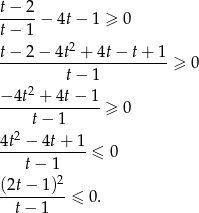
t-−-2 − 4t − 1 ≥ 0 t − 1 t − 2 − 4t2 + 4t− t + 1 ----------------------- ≥ 0 t − 1 −-4t2-+-4t−--1 t− 1 ≥ 0 2 4t--−-4t-+-1 ≤ 0 t− 1 (2t − 1)2 --------- ≤ 0. t − 1

Licznik jest nieujemny, a mianownik jest ujemny (bo 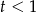t < 1 ), nierówność jest więc spełniona.

Wersja PDF