/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 7 marca 2015 Czas pracy: 180 minut
Zadania zamknięte
Liczba 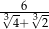 jest równa
jest równa
A) 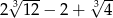 B)
B) 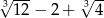 C)
C) 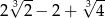 D)
D) 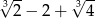
Okrąg o równaniu 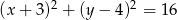 ma dwa punkty wspólne z prostą o równaniu
ma dwa punkty wspólne z prostą o równaniu
A) 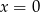 B)
B) 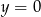 C)
C) 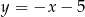 D)
D) 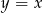
Jeżeli 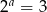 ,
, 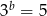 i
i 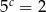 , to iloczyn
, to iloczyn 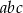 jest równy
jest równy
A) 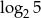 B)
B) 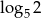 C) 1 D) 2
C) 1 D) 2
Największa wartość funkcji 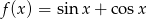 to
to
A) 1 B) 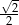 C)
C) 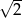 D) 2
D) 2
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie są dwie kule białe i 3 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 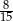 B)
B)  C)
C) 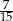 D)
D) 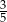
Zadania otwarte
Oblicz granicę ciągu 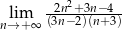 .
.
Funkcja 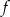 jest określona wzorem
jest określona wzorem 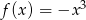 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania prostych stycznych do wykresu funkcji
. Wyznacz równania prostych stycznych do wykresu funkcji 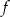 , które są równoległe do prostej
, które są równoległe do prostej 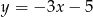 .
.
Na płaszczyźnie dany jest nieskończony ciąg 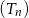 , dla
, dla 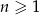 , równoramiennych trójkątów prostokątnych. Pole trójkąta
, równoramiennych trójkątów prostokątnych. Pole trójkąta 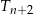 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 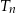 dla
dla 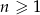 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 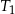 i
i 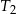 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Wykres funkcji 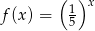 przesunięto najpierw o wektor
przesunięto najpierw o wektor ![→ v 1 = [2,− 6]](https://img.zadania.info/zes/0097788/HzesT37x.gif) , potem o wektor
, potem o wektor ![→v 2 = [− 3,7]](https://img.zadania.info/zes/0097788/HzesT38x.gif) , a na koniec o wektor
, a na koniec o wektor 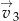 . W wyniku tej operacji otrzymano wykres funkcji
. W wyniku tej operacji otrzymano wykres funkcji 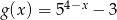 . Wyznacz współrzędne wektora
. Wyznacz współrzędne wektora 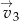 .
.
Oblicz sumę szóstych potęg pierwiastków równania 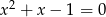 .
.
Podstawa trójkąta równoramiennego ma długość 10, a cosinus jednego z jego kątów jest równy 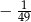 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
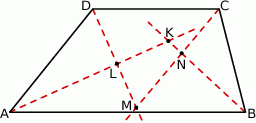
Dwusieczne kątów wewnętrznych trapezu 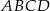 przecinają się w punktach
przecinają się w punktach 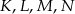 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 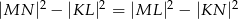 .
.
Funkcje 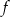 i
i 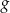 są określone wzorami:
są określone wzorami: 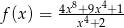 i
i 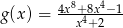 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wykaż, że
. Wykaż, że 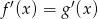 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 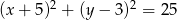 równoległych do prostej o równaniu
równoległych do prostej o równaniu 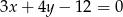 .
.
Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest nierówność
spełniona jest nierówność
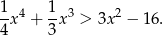
Wykaż, że 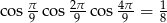 .
.
Środki ścian czworościanu foremnego 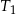 są wierzchołkami czworościanu
są wierzchołkami czworościanu 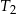 . Oblicz stosunek objętości czworościanów
. Oblicz stosunek objętości czworościanów 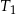 i
i 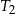 .
.
Oblicz prawdopodobieństwo warunkowe, że w czterokrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej dwie „dwójki”, pod warunkiem że otrzymamy co najmniej jedną „piątkę”.

