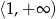Zadanie nr 9810360
Wyznacz dziedzinę funkcji określonej wzorem 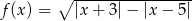 .
.
Rozwiązanie
Wyrażenie pod pierwiastkiem musi być nieujemne, czyli mamy do rozwiązania nierówność
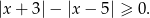
Sposób I
Jeżeli zapiszemy nierówność w postaci
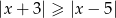
to obie strony są nieujemne i możemy nierówność podnieść stronami do kwadratu.
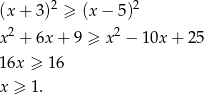
Sposób II
Wyrażenie pod pierwszą wartością bezwzględną zeruje się dla 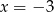 , a wyrażenie pod drugą dla
, a wyrażenie pod drugą dla 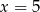 . Mamy więc do rozpatrzenia 3 przypadki.
. Mamy więc do rozpatrzenia 3 przypadki.
Jeżeli 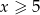 to mamy nierówność
to mamy nierówność
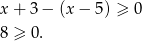
Nierówność jest oczywiście spełniona.
Jeżeli 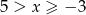 to mamy nierówność
to mamy nierówność
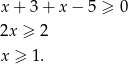
Mamy więc w tym przypadku 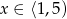 .
.
Jeżeli natomiast  to mamy nierówność
to mamy nierówność
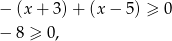
która jest sprzeczna.
Podsumowując, rozwiązaniem nierówności jest zbiór
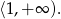
Odpowiedź: