Zadanie nr 9812821
Wykaż, że jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 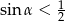 to
to 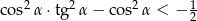 .
.
Rozwiązanie
Przekształcamy lewą stronę nierówności (korzystając ze jedynki trygonometrycznej i definicji tangensa).
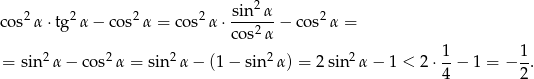
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 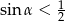 to
to 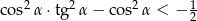 .
.
Przekształcamy lewą stronę nierówności (korzystając ze jedynki trygonometrycznej i definicji tangensa).