/Szkoła średnia

Zadanie nr 9814086

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapez wpisano okrąg. Punkt styczności okręgu z dłuższą podstawą trapezu dzieli tę podstawę na odcinki długości 2,5 dm i 4 dm. Wysokość trapezu ma długość 4 dm. Oblicz obwód tego trapezu.

Rozwiązanie

Zaczynamy od rysunku.

PIC

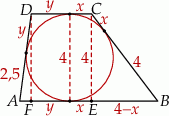
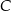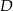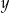Jeżeli oznaczymy odległości punktów C i D od punktów styczności z okręgiem przez x i y odpowiednio to z trójkąta prostokątnego 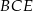BCE mamy

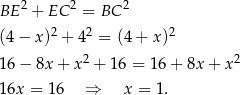
BE 2 + EC 2 = BC 2 2 2 2 (4 − x ) + 4 = (4+ x ) 16 − 8x + x2 + 16 = 16 + 8x + x 2 16x = 16 ⇒ x = 1.

Podobnie z trójkąta 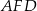AF D mamy

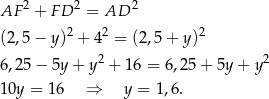
AF 2 + F D 2 = AD 2 2 2 2 (2,5 − y ) + 4 = (2,5+ y) 6 ,2 5− 5y+ y2 + 16 = 6,25 + 5y + y 2 1 0y = 16 ⇒ y = 1,6.

Zatem obwód trapezu jest równy

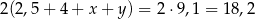
2 (2,5+ 4+ x+ y) = 2 ⋅9,1 = 18,2

 
Odpowiedź: 18,2 dm

Wersja PDF