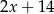/Szkoła średnia

Zadanie nr 9814447

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczba -7 jest miejscem zerowym 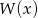W (x) . Wyznacz resztę z dzielenia tego wielomianu przez wielomian 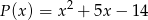P(x) = x 2 + 5x − 14 , jeśli wiadomo, że w wyniku dzielenia wielomianu 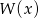W (x ) przez dwumian 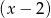(x − 2) otrzymujemy resztę 18.

Rozwiązanie

Sposób I

Oznaczmy szukaną resztę przez 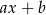ax + b , tzn.

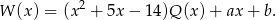
2 W (x ) = (x + 5x − 14)Q (x) + ax + b.

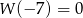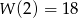Z podanych w zadaniu informacji wynika, że W (− 7) = 0 oraz W (2) = 18 . Mamy zatem układ równań

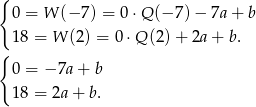
{ 0 = W (− 7) = 0 ⋅Q (−7 )− 7a + b 18 = W (2) = 0 ⋅Q (2)+ 2a+ b. { 0 = − 7a + b 18 = 2a+ b.

Odejmujemy od drugiego równania pierwsze (żeby skrócić 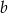b ) i mamy

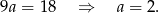
9a = 1 8 ⇒ a = 2.

Stąd 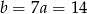b = 7a = 14 .

Sposób II

Z podanych informacji mamy

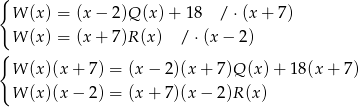
{ W (x) = (x− 2)Q (x)+ 18 / ⋅(x + 7) W (x) = (x+ 7)R(x ) / ⋅(x − 2) { W (x)(x + 7 ) = (x− 2)(x + 7)Q (x) + 18(x + 7) W (x)(x − 2 ) = (x+ 7)(x − 2)R (x)

Odejmujemy od pierwszego równania drugie i mamy

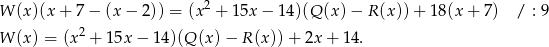
W (x)(x + 7 − (x − 2)) = (x2 + 15x − 14)(Q (x) − R (x))+ 18(x + 7) / : 9 W (x) = (x 2 + 1 5x− 14)(Q (x) − R (x))+ 2x+ 14.

Interesująca nas reszta jest więc równa 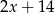2x + 1 4 .  
Odpowiedź: 2x + 14

Wersja PDF