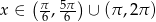Zadanie nr 9818560
Rozwiąż nierówność 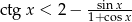 , gdzie
, gdzie 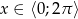 ;
;
Rozwiązanie
Aby napisana nierówność miała sens, musi być
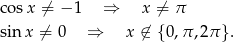
Druga nierówność jest potrzebna ze względu na dziedzinę 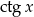 . Teraz przekształcamy podaną nierówność
. Teraz przekształcamy podaną nierówność
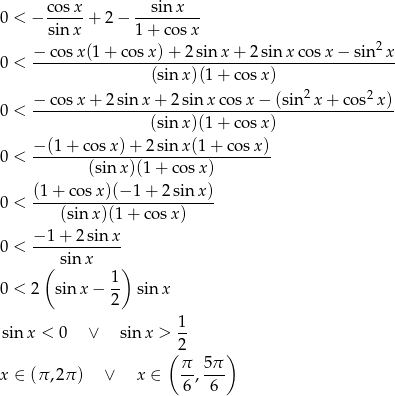
Odpowiedź: 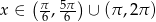
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 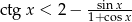 , gdzie
, gdzie 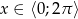 ;
;
Aby napisana nierówność miała sens, musi być
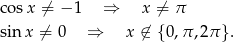
Druga nierówność jest potrzebna ze względu na dziedzinę 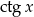 . Teraz przekształcamy podaną nierówność
. Teraz przekształcamy podaną nierówność
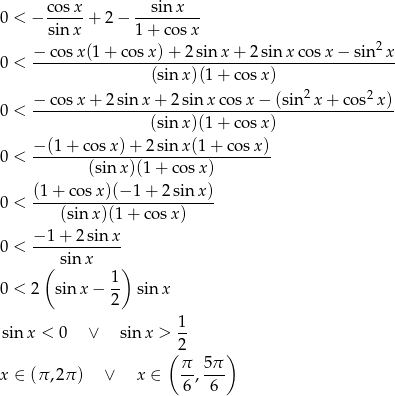
Odpowiedź: